
Here is the situation: The Falcons have the ball on the New England 23. It is 2nd and 11 with four minutes left, and the Falcons are nursing a 28 to 20 lead. Matt Ryan doesn’t hand it off! He gets sacked, putting the Falcons out of field goal range, and the rest is history, as the Patriots mount unarguably the best comeback in Super Bowl history. The Falcons made many mistakes managing the clock, like snapping the ball four times with more than ten seconds left on the play clock when they had the lead in the fourth quarter. However, I want to focus on one of the crucial plays that may have turned the game around for the Patriots. If you need a reminder, you can watch the play here. I will try to compare the probability of the Falcons winning the game given they run the ball versus pass the ball on second down.
The Run
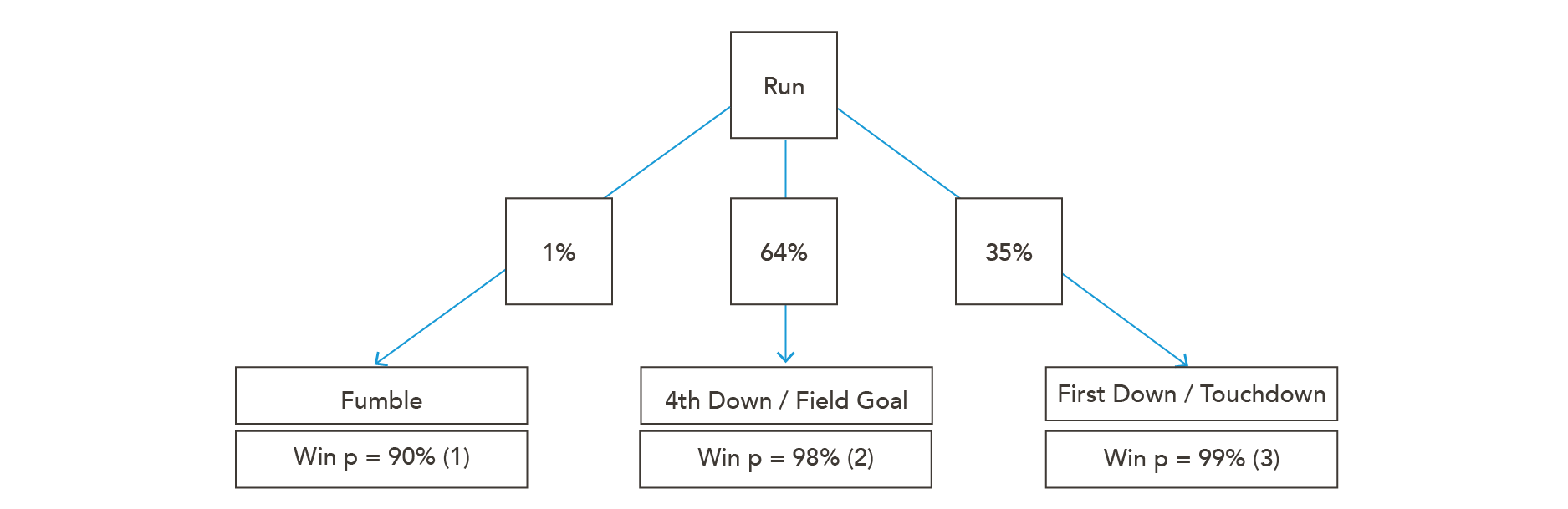
See more details for (1) Fumble, (2) 4th Down / Field Goal, and (3) First Down / Touchdown
If you run the ball twice, the most common outcomes are as follows: fumbling, not picking up the first down and then kicking a field goal, and getting a first down/touchdown. The probability of the Falcons not getting the first down and choosing to kick a field goal is roughly 64%. Admittedly, this is the hardest probability for me to predict because it involves assuming how the Patriots stack the box and their ability to stop the run, which they hadn’t been successful in doing most of the game. I will conduct a scenario analysis on this estimated probability later in the article. Above is a probability tree to help you visualize the different possibilities, showing the likelihood of each scenario and the win probability given each result of the drive.
The probability of the Falcons winning the game given they run the ball is therefore 1% *90% + 64%*98% + 35*99% = 98.27%.
The Pass
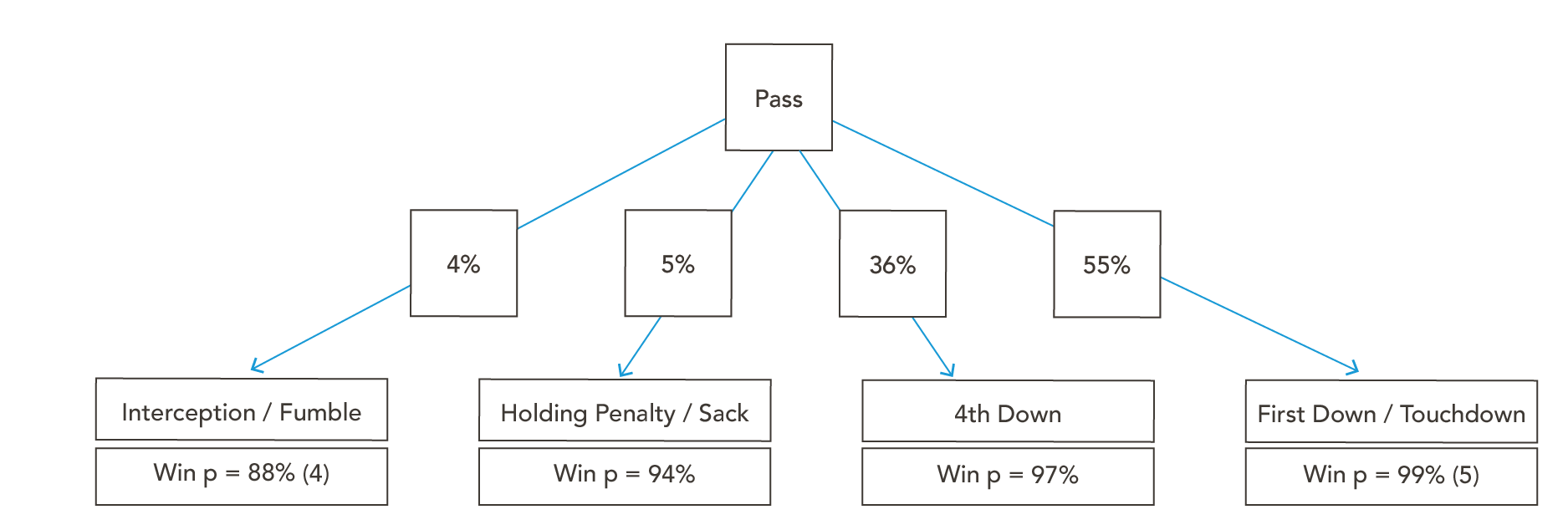
Now let’s discuss the probability of the Falcons winning the game given they pass the ball. The most common scenarios when they pass are a fumble/interception, sack/holding penalty that backs them up, an incompletion/completion short of the first down mark, and a first down/touchdown.
- The probability of an interception is around 2%((“NFL Team Opponent Interceptions Thrown Percentage.” TeamRankings.com. Accessed 17 Feb. 2017.)) and fumbling and not recovering is roughly 1%((Burke, Brian. “Fumble Rates by Play Type.” Advanced Football Analytics. Accessed 17 Feb. 2017.)), so the probability of a turnover is 3% per play. Sometimes, the Falcons might pass once and then run, so I would estimate the expected number of passes is 1.4 in that four down set given they pass on 2nd and 11. Therefore, the Falcons have a roughly 4% chance of turning the ball over.
- The probability of a sack/holding penalty to back up the Falcons is roughly 5% (5%((“NFL Team QB Sacked Percentage.” TeamRankings.com. Accessed 17 Feb. 2017.)) chance of a sack per play, 2%((“Offensive Holding – 2016.” NFL Penalty Stats Tracker. Accessed 17 Feb. 2017.)) chance of a holding penalty per play, but there is a good chance they get the yardage back on the subsequent play if the setback is on 2nd down).
- The probability of the Falcons picking up the first down after passing on 2nd and 11 is 55%. (Therefore, the probability of them not getting the first down without an interception/fumble or holding penalty/sack is 36%; 1 – the probability of the other scenarios). This is also the hardest probability to predict because we must assume they do not turn the ball over or get sacked/take a penalty. I run a scenario analysis on this later in the article as well.
Given the Falcons don’t get the first down but also do not get backed up, the probability of them winning should be slightly lower (I estimate 97%) than if they run the ball, as there will be on average more time left on the clock for the Patriots to potentially come back.
I estimate 94% for the probability of the Falcons winning given a holding penalty/taking a sack because it is between the fumble in the run scenario (90%) and them not getting the first down in the pass scenario, but also not having a penalty/sack (97%). In this 5% scenario, the Falcons will be forced to kick a longer field goal or potentially punt. As we move the 94% win probability 1% each direction, it will only move the total win percent .05%, so it is not a big deal if this number is slightly off. Above is a probability tree to help you visualize the pass scenario showing the likelihood of each outcome and the win probability given the result of the drive.
Therefore, the probability of the Falcons winning the game given they throw the ball on 2nd and 11 is 4% * 88% + 5% * 94% + 36% * 97% + 55%* 99% = 97.59%.
Scenario Analysis
From looking at that analysis, it seems like the run is the better play (98.27% versus 97.59%).
However, let’s see what happens if we move around the main variable for the result of the drive: getting a first down given you run it twice (currently 35%) and the scenario of getting a first down given you pass it on 2nd and 11 (currently 55%).


Looking at the scenario analysis above, it seems hard to find a situation in which passing the ball is better than running the ball (they do obviously exist). All of the probabilities in the assumptions I make can be tweaked; they are just my best estimates. Feel free to put in your own and see what you come up with. Let me know in the comments what you find.
Conclusion
We see here that the decision to pass the ball on 2nd and 11 was most likely an incorrect one, although it may not be as obvious as everyone else thought it was. While .68% (the difference I estimate between win probabilities from running versus passing) is not a whole lot in absolute terms, the relative difference is huge!
With these assumptions, the Falcons choosing to pass led to the Patriots having a 2.41% chance to win the game, whereas the Falcons could have left the Patriots with a 1.73% chance by choosing to run – a relative difference of almost 40%.
(Photo of Kyle Shanahan, above, used under CC0 1.0 / modified from original)




Subscribe Now
Get each new post sent straight to your inbox