Rooting for the Favorite

Imagine this hypothetical scenario: The Patriots have advanced to the AFC Championship game against the Chiefs and are waiting to see who will play the Falcons in the NFC Championship game. The Eagles are playing the Packers in the divisional round for the right to play the Falcons in the NFC Championship. The team that wins the NFC Championship will play the winner of the AFC Championship in the Super Bowl. The Falcons are 90% to beat the Eagles and 75% to beat the Packers. The Patriots and Falcons are teams of exactly equal strength. Therefore, in the Super Bowl the Patriots are 90% to beat the Eagles, 75% to beat the Packers, and 50% to beat the Falcons.

The chart below shows the different possible matchups with the winning probabilities for each game assuming the Patriots end up beating the Chiefs.

As long as we’re imagining scenarios, picture this: Tom Brady is sitting at home watching that Eagles vs. Packers game. The Eagles score a game-winning touchdown and Tom Brady is excited he won’t have any chance of facing the better Packers team. Gisele Bündchen shakes her head in disgust at her husband and says that she was rooting for the Packers.

Which team would you be rooting for if you were on the Patriots and wanted to maximize your chances of winning the Super Bowl? Team Gisele Bündchen rooting for the Packers, or Team Tom Brady rooting for the Eagles?

While your initial gut reaction may tell you to go with the Eagles, the correct team to root for is the Packers. If you picked Team Tom Brady you’re going to feel deflated. Take a moment to think it over. The probability the Patriots win the super bowl after they’ve beaten the Chiefs is as follows:

P(Win)=P(Falcons win NFC)*P(Patriots beat Falcons)+P(Falcons lose NFC)*P(Patriots win against team that beat Falcons in the NFC)

Looking at the scenario where the Packers beat the Eagles:
Patriots will play the Falcons 75% of the time and win that game 50% of the time.
Patriots will play the Packers 25% of the time and win that game 75% of the time.
P(Win Super Bowl) = 75% * 50% + 25% * 75% = 56.25%

If the Eagles beat the Packers and Patriots beat the Chiefs:
Patriots will play the Falcons 90% of the time and win that game 50% of the time.
Patriots will play the Eagles 10% of the time and win that game 90% of the time.
P(Win Super Bowl) = 90% * 50% + 10% * 90% = 54%

Looking at a more general case:
If x equals the probability the Falcons win against a team in the NFC game, then the probability that the Patriots beat that same team is also x. Therefore, the probability that the Patriots win the Super Bowl after beating the Chiefs is equal to:

P(win)=(0.5)*x+(1-x)*x
P(win)=1.5x-x^2

Taking the derivative with respect to x and setting equal to 0, we get:

1.5-2x=0
x=0.75

If the Patriots are of equal strength to the Falcons, they want the Falcons to have a 75% chance to win the NFC Championship game. The Patriots want to play a weaker team in the Super Bowl. The weaker the opposing team, the lower chance the Patriots have of getting to play them. Below is a graph that shows the Patriots chances to win the Super Bowl vs the Falcons chances to win the NFC. (Assuming the two teams are equal)

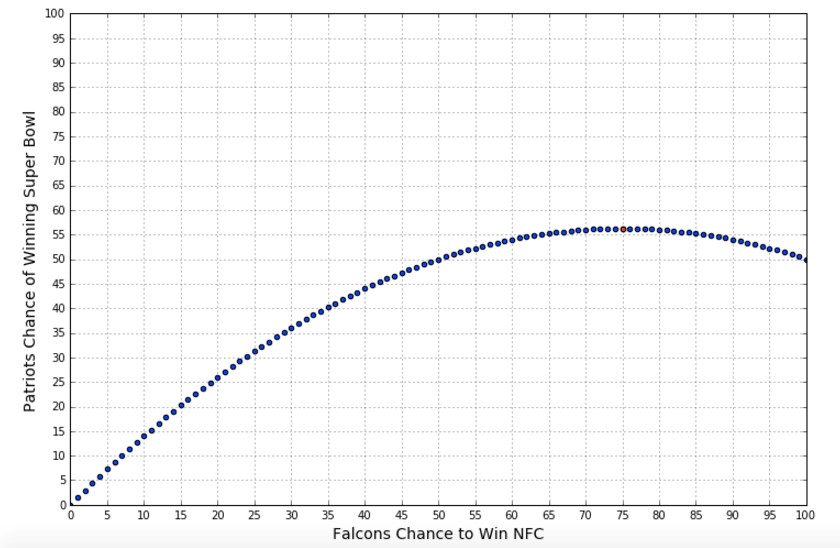
This is an example of a question where your initial “gut” response is often going to be wrong. It seems unintuitive to want the stronger team to win. This is a situation where you need to slow down and think carefully. After doing the math, you clearly prefer a 56.25% chance of winning to a 54% chance. Sometimes it is right to trust your gut, this situation isn’t one of them.