One of my favorite elements of two player games is the doubling cube, which is typically used playing backgammon. A game begins with stakes of one point, but each player has the option to double the stakes before any of their turns. If Player 1 proposes a double, Player 2 has the option of accepting the double and playing the game for two points, or declining the double, resigning, and allowing Player 1 to win one point. If Player 2 accepts, then Player 2 ‘owns‘ the cube going forward – Player 2 may redouble before any of his turns, while Player 1 may not. If Player 1 accepts a redouble by Player 2, then the game will be worth four points, and Player 1 would take possession of the cube.
Options always have non-negative value, and when gaming with a cube, the option to double the stakes provides tremendous value. We can demonstrate this value for backgammon by calculating a player’s expected points (equity) with and without the doubling cube (‘cubeful equity’ and ‘cubeless equity’ respectively) for some simple endgame scenarios.
Let’s start with a scenario where, unless they roll doubles, either player needs two rolls to win the game (if either rolls doubles, they win immediately):
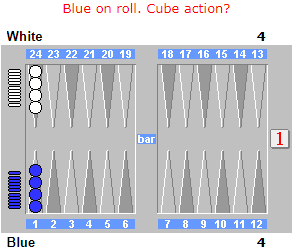
What is Blue’s cubeless equity?
Answer: In order for White to win, Blue needs to roll singles followed by White rolling doubles. This will occur with probability 5/6 * 1/6 = 5/36. Blue’s cubeless equity is (31/36 * 1 + 5/36 * (-1) = 26/36 = ~.722.
But of course, with this large advantage, Blue would like to raise the stakes. If the cube is available, Blue should double. If White accepts, Blue’s equity would be 1.444 (note that White would have no opportunity to profitably redouble). White should pass, and allow Blue to gain one point. On this winning board, the option to double increases Blue’s equity by .278 points!
Moving on to a more complex, three-roll scenario:
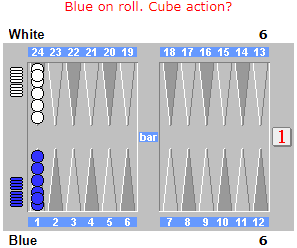
What is Blue’s cubeless equity?
Answer: If Blue rolls doubles on either of her first two rolls, she guarantees a win. If both players roll singles to start, we know that Blue’s cubeless equity is .722 from the previous example. Otherwise, Blue loses by rolling singles twice when White opens with doubles. Overall, Blue’s cubeless equity is 0.576:
| Probability | Equity | |
|---|---|---|
| D | 0.167 | 1 |
| SDD | 0.023 | 1 |
| SDS | 0.116 | -1 |
| SS | 0.694 | 0.722 |
| Weighted Average: | 0.576 | |
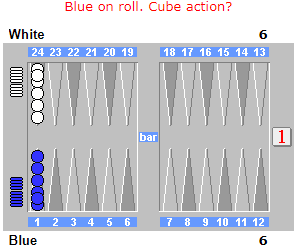
Now let’s bring the cube back into consideration. If Blue decides not to double now, what is her equity?
Answer: Note that, again, White never has a profitable opportunity to double/redouble – the only time White is ahead before he rolls, he’s already in a position guaranteed to win. If both players open singles, we discussed above that Blue would like to double, and White should pass. The option to double increases Blue’s equity to 1 in that scenario, and increases Blue’s overall equity to 0.769:
| Probability | Equity | |
|---|---|---|
| D | 0.167 | 1 |
| SDD | 0.023 | 1 |
| SDS | 0.116 | -1 |
| SS | 0.694 | 1 |
| Weighted Average: | 0.769 | |
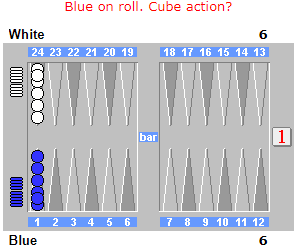
If Blue does double now, what’s her equity?
Answer: If White accepts, Blue’s equity would be 2*0.576=1.151. White should pass, so Blue’s cubeful equity is 1 – an improvement of 0.424 points over her cubeless equity!
Can you solve the four-roll endgame?
This scenario is more complex, and it’s now possible that White will double or redouble if he rolls better than Blue. What is Blue’s cubeless equity? Should Blue double now, or wait a roll? If she doubles, should White accept? How much value does each player gain from the option to double?
(Click here to show answer)
Answers: Blue’s cubeless equity is .4905.
If Blue doesn’t double now, Blue’s cubeful equity is .7608 (Blue will probably double next turn). Blue should double now, White should take, and Blue’s cubeful equity is .9168 (.4262 more than her cubeless equity). If White doesn’t have the option to redouble, White should still take, but barely – Blue’s cubeful equity would rise to .9811 (White’s option to redouble is worth .0643).
If White controls the cube, Blue’s equity would be only .4584 (White’s option to double is worth .0322 over his cubeless equity).
So why do we care about solving these relatively simple examples? While real games hardly ever end with these exact boards, it’s useful to be familiar with the results of many “reference positions.” Knowing the win probabilities for these positions gives you a baseline to evaluate related positions in real time. Now you know that a three-roll endgame is a resounding double/pass, while the four-roll endgame is a clear double and a more marginal take.
Thinking about doubling more generally: what is the minimum (cubeless) probability of winning that White needs to accept a double:
If White is not allowed to redouble?
(Click here to show answer)
Answer: 25%, because .25*(2) + .75*(-2) = -1, which is White’s equity when he passes
If unlimited redoubling is allowed?
(Click here to show answer)
Answer: If you model win probabilities as a continuous random walk, and assume you can double at any time, the answer would be 20%. However, Backgammon is a discrete game, whose dynamics are much more difficult to solve than a continuous random walk. Gammons also play a large roll in whether White should accept the double. There are boards when White should pass with win probability over 20%, and boards when he should take with probability under 20%.
Backgammon World Champion and former SIG trader Frank Frigo points out that you can (in theory) take with as low as 18.75% winning chances in a money game when you have full efficiency of the redouble. A classic example of this would be a situation where each player has one checker remaining on their 6 point. It is a double and exactly a borderline take/pass because the taker gets full value on a redouble when the initial doubler misses with 9/36 of his numbers and then you win with 27/36 (also a borderline take/pass).
Related Posts
Board Gaming for 2 Players or Less
As you may know, board games are a popular activity here at SIG. Last year, our Dublin office even launched an official board games social club, where we regularly meet after work for sessions of a variety of games, including some of those discussed in other blog posts.
Unfortunately […]
Shut Up & Sit Down Game Recommendations
Finding the perfect gift can be tricky. As minimalist sensibilities have continued to power pop culture (think Marie Kondo, mid-century modern furniture, and experiences over objects) the landscape has become even more daunting.
What if I told you, dear readers, that there […]
Crucial Games and Tactics for SIG’s 1st Place NACCL Chess Team
Over 6 Thursdays in late January and February, the inaugural online North American Corporate Chess League took place, with over 400 players and 40 teams competing on lichess.org. The league awarded prizes to both the top 15 individuals and the top 5 teams, with each team’s […]
Subscribe Now
Get each new post sent straight to your inbox